GEOMETRY R
Unit 13 – Circles
Date
Classwork
Day
Assignment
Wednesday
3/28
Constructions Project
Constructions Project Due
4/24
Thursday
3/29
Constructions Project
3/30 – 4/6
No School
Monday
4/9
Central angles
Inscribed Angles
1
HW 13.1
Tuesday
4/10
Central angles
Inscribed Angles (Day 2)
1.5
HW 13.1 Part 2
Wednesday
4/11
Arcs and Chords
2
HW 13.2
Thursday
4/12
Area of Sectors and Area problems
Arc Length
3
HW 13.3
Friday
4/13
Tangents
Unit 14 Quiz 1
4
HW 13.4
Monday
4/16
Secants, Tangents, and Angle Measures
5
HW 13.5
Tuesday
4/17
Lengths of Secant Segments, Tangent
Segments, and Chords
6
HW 13.6
Wednesday
4/18
Writing Equations of Circles
(Standard Form)
Unit 14 Quiz 2
7
HW 13.7
Thursday
4/19
Equations of Circles
(General Form)
8
HW 13.8
Friday
4/20
Inscribed and Circumscribed Polygons
Unit 14 Quiz 3
9
HW 13.9
Monday
4/23
Review
12
Constructions Project Due
4/24
Review Sheet
Tuesday
4/24
Review
13
Review Sheet
Wednesday
4/25
Unit 14 Test
14

Examples
Find the value of x.
a. b. c.
Words
Figure
Two circles are congruent circles if and
only if they have congruent radii.
Concentric Circles are coplanar circles that
have the same center.
Sum of Central Angles
Words
Example
The sum of the measures of the central angles of a circle
with no interior points in common is 360 degrees.
CIRCLES, ARCS, ANGLES, AND CHORDS [1]
A circle is the locus or set of all points in a plane equidistant
from a given point called the center of the circle.
A central angle of a circle is an angle whose vertex is the
center of the circle. Its sides contain two radii of the circle.

Arc
Figure
Minor Arc is the shortest arc connecting
two endpoints on a circle
Major Arc is the longest arc connecting
two endpoints on a circle
Semicircle is an arc with endpoints that
lie on a diameter
The measure of an arc of a circle is equal
to the measure of its corresponding
central angle.
Examples
GJ
is a diameter of circle K. Identify each arc as a major arc, minor arc, or semicircle. Then find
its measure.
a. m
GH
b. m
GLH
c. m
GLJ
Congruent arcs are arcs in the same or congruent circles that have the same measure.
Words
Example
Figure
In the same circle or in congruent
circles, two minor arcs are congruent
if and only if their central angles are
congruent.
An arc is a portion of a circle defined by two endpoints. A
central angle separates the circle into two arcs with measures
related to the measure of the central angle.

Adjacent arcs are arcs that have exactly one point in common.
Examples
Find each measure in circle F.
a. m
AED
b. m
ADB
Case 1
Case 2
Case 3
Examples
Find each measure.
a. b.
Arc Addition Postulate
Words
Example
Figure
The measure of an arc formed by two
adjacent arcs is the sum of the
measures of the two arcs.
Inscribed Angle Theorem
Words
Example
Figure
If an angle is inscribed in a circle, then the
measure of the angle equals one half the
measure of its intercepted arc.
An inscribed angle has a vertex on a circle and sides that contain
chords of the circle. An intercepted arc has endpoints on the sides of
an inscribed angle and lies in the interior of the inscribed angle.

c.
d.
Examples
a. Find
mT
b. If
mS
= 3x and
mV
= x + 16, find
mS
.
Thales’ Theorem
Words
Examples
Figures
An inscribed angle of a triangle
intercepts a diameter or semicircle if
and only if the angle is a right angle.
Examples
1. a. Find
mF
.
b. If
mF
= 7x + 2 and
mH
= 17x – 8, find x.
Words
Example
Figure
If two inscribed angles of a circle intercept
the same arc or congruent arcs, then the
angles are congruent.

2. In the figure below,
is the diameter of a circle of radius miles. If
miles, what is ?
3. In the circle shown,
is a diameter with center .
a. Find .
b. Find .
c. Find .
4. Rectangle is inscribed in circle . Boris says that diagonal could pass through the
center, but it does not have to pass through the center. Is Boris correct? Explain your
answer in words, or draw a picture to help you explain your thinking.

5. Prove that in the diagram provided.
6. Find the measures of the labeled angles.
a.
b.
c.
d.

Find the value in each figure below, and describe
how you arrived at the answer.
1. Hint: Thales’ theorem
2.
3.

ARCS AND CHORDS [2]
Examples
a. In the figures, circle J circle K and
MN PQ
. Find PQ.
If a line, segment, or ray divides an arc into two congruent arcs, then it bisects the arc.
Bisecting Arcs and Chords
Words
Examples
Figures
If a diameter (or radius) of a circle is
perpendicular to a chord, then it
bisects the chord and its arc.
If a diameter (or radius) of a circle
bisects a chord, then it must be
perpendicular to the chord.
Words
Example
In the same circle or in congruent circles, two minor arcs are
congruent if and only if their corresponding chords are
congruent
Arcs between parallel chords are congruent.
In a circle, central angles are congruent if and only if their
corresponding chords are congruent.

Examples
a. In circle S,
mPQR
= 98. Find
mPQ
.
b. In circle S, find PR.
Examples
1. In circle A, WX = XY = 22. Find AB.
2. In circle H, PQ = 3x – 4 and RS = 14. Find x.
3. Given circle shown, and . Find .
Words
Example
Figure
In the same circle or in congruent
circles, two chords are congruent if
and only if they are equidistant from
the center.

4. In the figure, circle has a radius of .
.
a. If , what is the length of ?
b. If , what is the length of ?
5. Find the angle measure of
and
.
6.
and
. Find
a.
b.
c.
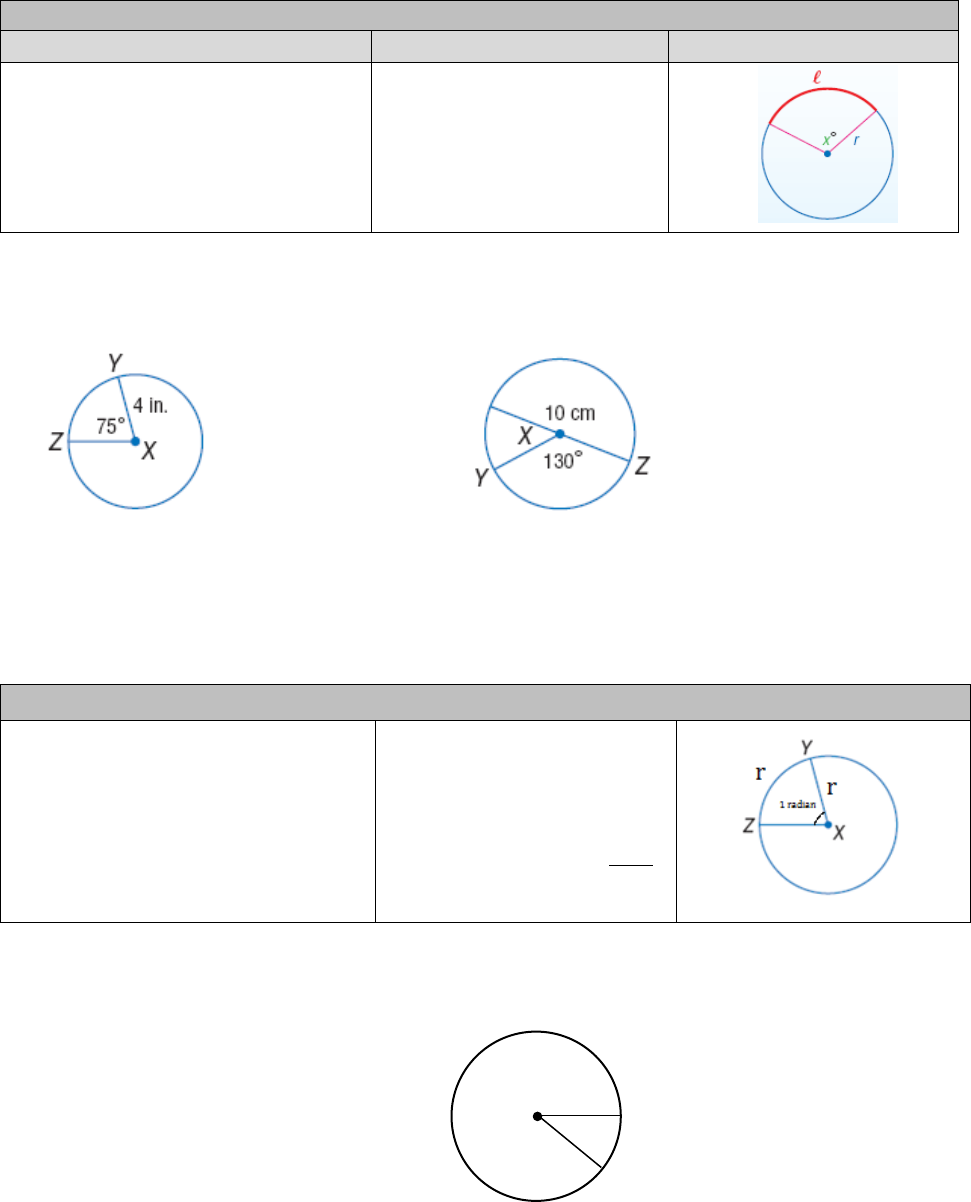
ARC LENGTH AND AREA OF SECTORS [3]
Arc length is the distance between the endpoints along an arc measured in linear units. Since an
arc is a portion of a circle, its length is a fraction of the circumference.
Examples
Find the length of
. Round to the nearest hundredth.
a. b.
1. Convert 120° to radians. 2. What is the measure of angle B, in radians?
Arc Length
Words
Proportion
Figure
The ratio of the length of an arc L
to the circumference of the circle
is equal to the ratio of the degree
measure of the arc to 360.
Radian Measure
A radian is the measure of the
central angle of a sector of a circle
with arc length of one radius
length.
π radians = 180°
To convert degrees to
radians, multiply by
180
2π
10
B

The area of a circle is found by using the formula
. A sector is a pie-shaped portion of the
circle enclosed by 2 radii and the edge of the circle. A central angle of a sector is an angle whose
vertex is at the center of the circle and crosses the circle.
Examples
a. Find the area of the sector shown at the right.
b. Find the area of a sector if the circle has a radius of 10 centimeters and the central angle
measures 72.
c. Find the area of a sector if the circle has a radius of 5 inches and the central angle
measures 60.
d. If the area of a sector is 15π square centimeters and the radius of the circle is 5
centimeters, find the measure of the central angle.
e. Find the measure of the central angle that intercepts a sector that is
the area of the
circle.
Area of Sectors
Words
Proportion
Figure
The area of a sector is
proportional to the part that the
central angle is of 360°.

1. is an equilateral triangle with edge length cm. , ,
and are midpoints of the sides. The vertices of the triangle
are the centers of the circles creating the arcs shown. Find
the following (round to the nearest hundredth):
a. The area of the sector with center .
b. The area of triangle .
c. The area of the shaded region.
d. The perimeter of the shaded region.
2. In the figure shown, cm,
cm, and . Find the
area in the rectangle, but outside of the
circles (round to the nearest hundredth).

TANGENTS [4]
Examples
a.
JL
is a radius of circle J. Determine whether
KL
is tangent to circle J. Justify your
answer.
b.
JH
is tangent to circle G at J. Find the value of x.
c. Find the value of x. Assume that segments that appear to be tangent are tangent.
Theorem
Words
Example
Figure
In a plane, a line is tangent to a circle if
and only if it is perpendicular to a
radius drawn to the point of tangency.
A tangent is a line in the same plane as a circle that intersects the circle in
exactly one point, called the point of tangency. A common tangent is a
line, ray, or segment that is tangent to two circles in the same plane.
M

Examples
a.
AB
and
CB
are tangent to circle D. Find the value of x.
b. Find the value of x. Assume that segments that appear to be tangent are tangent.
Circumscribed Polygons
Examples
a. Quadrilateral RSTU is circumscribed about circle J. If the perimeter is 18 units, find x.
Theorem
Words
Example
Figure
If two segments from the same
exterior point are tangent to a
circle, then they are congruent.

SECANTS, TANGENTS, AND ANGLE MEASURES [5]
Examples
Find x.
a. b.
c. d.
Theorem
Words
Example
Figure
If two secants or chords intersect in
the interior of a circle, then the
measure of an angle formed is one half
the sum of the measure of the arcs
intercepted by the angle and its
vertical angle.
A secant is a line that intersects a circle in exactly two points. When two
secants intersect inside a circle, the angles formed are related to the arcs
they intercept.

Examples
Find each measure.
a. b.
Examples
Find each measure.
a. b.
Theorem
Words
Example
Figure
If a secant and a tangent intersect at
the point of tangency, then the
measure of each angle formed is one
half the measure of its intercepted arc.
Theorem
If two secants, a secant and a tangent, or two tangents intersect in the exterior of a circle,
then the measure of the angle formed is half the difference of the measures of the
intercepted arcs.

Find and/or .
1.
2.

LENGTHS OF TANGENT SEGMENTS, SECANT SEGMENTS, AND CHORDS [6]
Examples
Find x.
1. 2.
3. 4.
A secant segment is a segment of a secant line that has exactly one
endpoint on the circle. A secant segment that lies in the exterior of the
circle is called an external secant segment.
Theorem
Words
Example
Figure
If two chords intersect in a circle, then
the products of the lengths of the chord
segments are equal.
When two chords intersect inside a circle, each chord is divided into two segments,
called chord segments. In the figure, chord
AC
is divided into segments
AB
and
BC
. Likewise, chord
ED
is divided into segments
EB
and
BD
.

Examples
Find x.
1. 2.
3.
An equation similar to the one above can be used when a secant and a tangent intersect outside a
circle. In this case, the tangent segment, or segment of a tangent with one endpoint on the circle,
is both the exterior and whole segment.
Find x.
1. 2.
Theorem
Words
Example
Figure
If two secants intersect in the exterior of a
circle, then the product of the measures of
one secant segment and its external secant
segment is equal to the product of the
measures of the other secant and its external
secant segment.
Theorem
Words
Example
Figure
If a tangent and a secant intersect in the
exterior of a circle, then the square of the
measure of the tangent is equal to the
product of the measures of the secant and its
external secant segment.

EQUATIONS OF CIRCLES (STANDARD FORM) [7]
Examples
Write the equation of each circle.
a. center at (1, -8), radius 7
b. the circle graphed at the right
c. center at origin, radius
d. Center at (4, -1), diameter 8
Equation of a Circle – Center-Radius/Standard Form
Words
Figure
The standard form of the equation of a circle with
center (h, k) and radius r, is (x – h)
2
+ (y – k)
2
= r
2
.
(Center-Radius Form)
Since all points on a circle are equidistant from the center, you can find an
equation of a circle by using the Distance Formula.
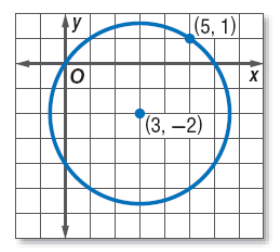
Examples
Write the equation of each circle.
a. center at (-2, 4), passes through (-6, 7)
b. the circle graphed at the right
c. center at (5, 4), passes through (-3, 4)
d. center at (-3, -5), passes through (0, 0)
e. The equation of a circle is (x – 4)
2
+ (y + 1)
2
= 9. State the center and the radius. Then graph
the equation.
EQUATIONS OF CIRCLES (GENERAL FORM) [8]
a. Express
as a trinomial.
b. Express
as a trinomial.
c. Factor the trinomial:
.
d. Complete the square to solve the following equation:
(Use a visual representation to support your work).
Sometimes equations of circles are presented in simplified form. To easily identify the center and
the radius of the circle, we sometimes need to factor and/or complete the square in order to
rewrite the equation in its center-radius or standard form.
1. Rewrite the following equations in the form
.
a.
b.
2. What is the center and radius of the following circle?

3. Identify the center and radius for each of the following circle.
a.
b.
4. Could the circle with equation
have a radius of 4? Why or why not?
5. Stella says the equation
has a center of (4, -1) and a radius of 5. Is
she correct? Why or why not?
6. Identify the graphs of the following equations as a circle, a point, or an empty set.
a.
b.
c.

INSCRIBED QUADRILATERALS [9]
Given: Cyclic quadrilateral ABCD
Prove: x + y = 180°
Examples
a. Quadrilateral WXYZ is inscribed in circle V. Find
mX
and
mY
.
b. Quadrilateral PQRS is a cyclic quadrilateral. Explain why
Theorem
Words
Example
Figure
If a quadrilateral is inscribed in a circle
(cyclic quadrilateral), then its opposite
angles are supplementary.

CONSTRUCTING INSCRIBED POLYGONS

